Simulating a mechanical system using rpg_core.js

This post is the continuation of the last post.

If you visit the page I have just created, you may find the simulation of a mechanical system.

Result of simulation

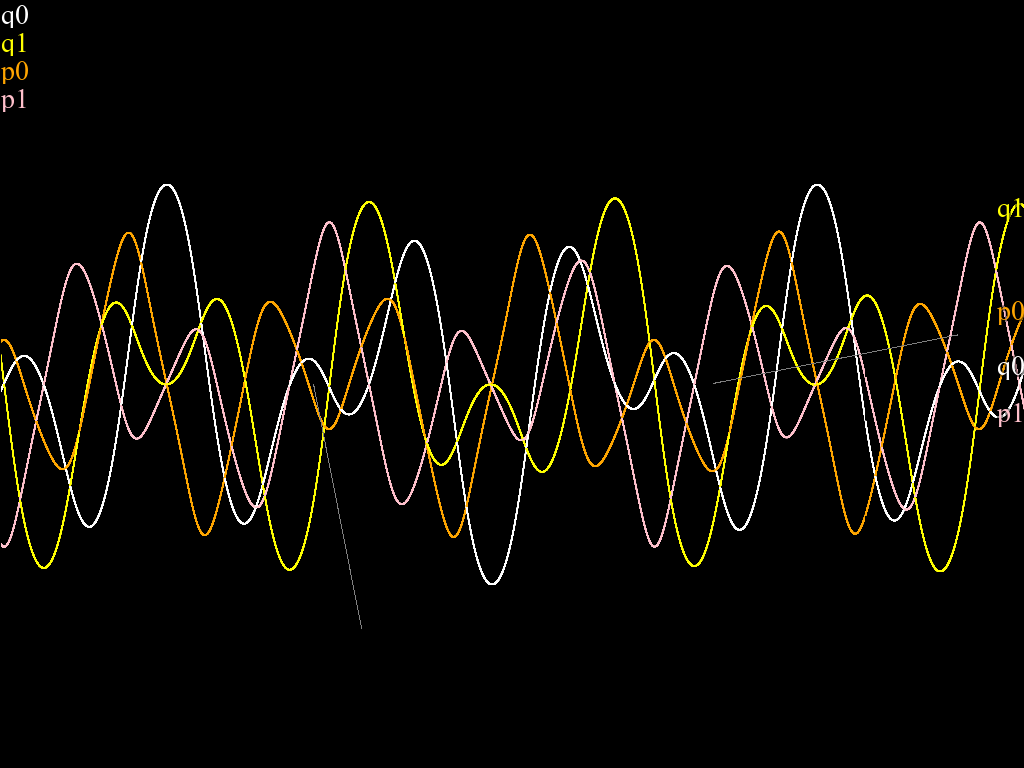
It is currently $$\mathcal H=p_1^2+p_2^2-\cos q_1-\cos q_2- \cos\!\left(q_1-q_2\right)$$ depicting two pendulum coupled with a spring (with $l_1=l_2$ and $m_1=m_2$, and the original length of the spring is zero, and the two hanging points overlap),

Spring-coupled pendulums

which is a classical example of non-linearly coupled system.

The pattern of the oscillation can be analyzed using discrete Fourier transformation, whose result can be found by clicking the buttons in the up-left corner (after the simulator has detected a period).

Result of DFT

Hitting the space bar can make the simulation pause.

If you want to use it to simulate other mechanical systems, you can study the codes I wrote and write your own codes in the console.

By the way, the OpenRGSS version of the simulator is open-source here. Please star the repo if you like it.